A* Algorithm
가장 대표적인 길찾기 알고리즘이다.
가중치를 기준으로 길을 찾는다.
알고리즘의 원리는 다음과 같다. 찾을 영역(Grid)를 만든다.
현재 경로에 대한 8방향(주위) 경로에 대한 가중치(비용)을 계산한다.
이때 경로를 계산하는 비용은 (F = G + H) 로 가정한다.
G = 시작점 으로부터 종료점까지 이동하는데 소요되는 비용
H = 현재 사각형에서 종료점까지의 예상 이동비용(이때는 방해물에 대한 계산을 처리하지 않고 가로세로만 계산한다.)
F = 현재까지 이동한 총 비용 ( G + H )
이동은 가로세로만 가능한것을 기준으로 설명한다.

현재 위치를 기준으로 가중치에 대한 처리를 한다. 시작점을 기준으로 오른쪽의 사각영역에 대한 계산을 하면 다음과 같다.
F = 40 ( 총합)
G =10 (시작점에서 가로 1칸 )
H =30(종료점까지의 가로 3칸)
이런식으로 주위의 탐색노드를 가중치 처리한다. 이때 대각선은 14를 사용한다.
이렇게 현재위치에서 8방향(모든방향)을 체크한 이후에 가장 작은 비용인(F)의 위치를 다시 선택한다.
그리고 다음과 같이 다시 재탐색한다.
-
선택한 사각형 '열린목록'에 넣고 '닫힌 목록'에 넣어준다.
-
인접한 위치을 확인한다. '닫힌목록'에 존재하거나 갈수없는곳(방해물, 끝)은 패스한다. 열린 목록에 해당 위치가 없다면 다시 '열린목록'에 추가하고 현재 위치를 새로운 탐색 위치로 변경한다.
-
인접한 탐색 목록이 이미 '열린목록'에 포함된 영역일경우 탐색 비용이 더 낮으면 교체한다.
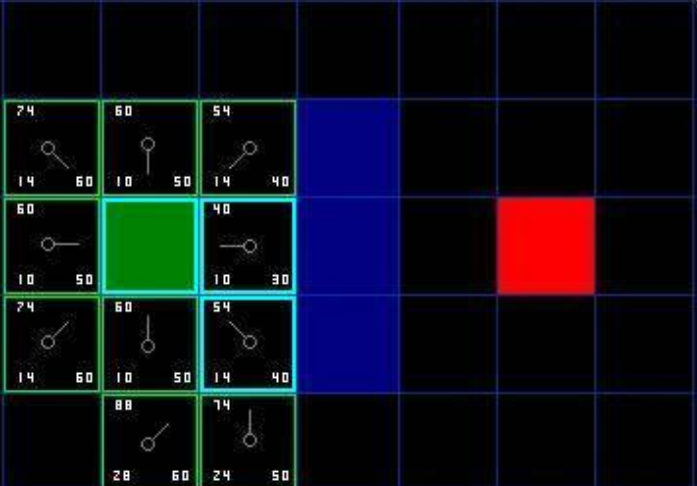
가장 비용이 낮은 오른쪽(40)은 더 이상 진행이 안되니 다음 열린 목록의 리스트로 넘어간다.
이때 오른쪽위(54),오른쪽 아래(54)가 동등합니다. 이럴때는 상관없이 탐색합니다.
오른쪽 아래가 기준이 되서 다시 재탐색을 하는 상황을 가정합니다. 이미 열린 노드에 포함된 노드들은 넘어가고 포함되지 않은 노드 를 탐색하고 열린노드에 넣는다. 이런식으로 탐색과정을 반복한다.
이때 비용이 변경되는 경우가 존재한다. 시작점에서 아래아래에 있는 영역을 보면
기존에 계산된 비용이 88이었으나 다시 탐색하는과정에서 80으로 변경되는 경우가 발생한다. 더 적은 비용이 계산되는 순간 다시 비용을 계산한다는 룰에 의거해 변경된 것이다.
A* 알고리즘의 주 목적은 가장 적은 비용을 탐색하는 것을 목적으로 하기 때문에 더 효율적인(적은)비용이 발생하면 교체를 해서 가장빠른 탐색경로를 찾는 것이다.
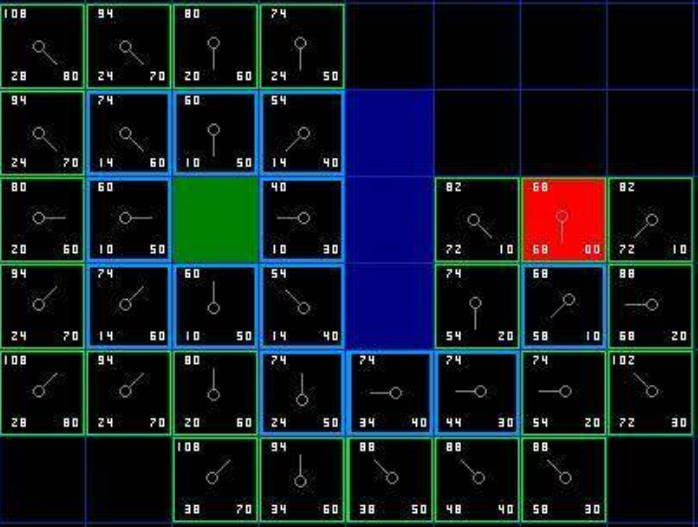
이런식으로 탐색을 하게되면 탐색한 경로를 기준으로 역순으로 다시 탐색한 경로를 되돌려주면 된다.
영상으로 보면 다음과 같다,
해당 이론을 가지고 실제 프로그래밍 적으로 구현하면 다음과 같다.
검색은 큐브가 시작점 빨간색 큐브가 종료점, 방해물은 분홍색 영역 으로 가정하고 구현한 결과이다.
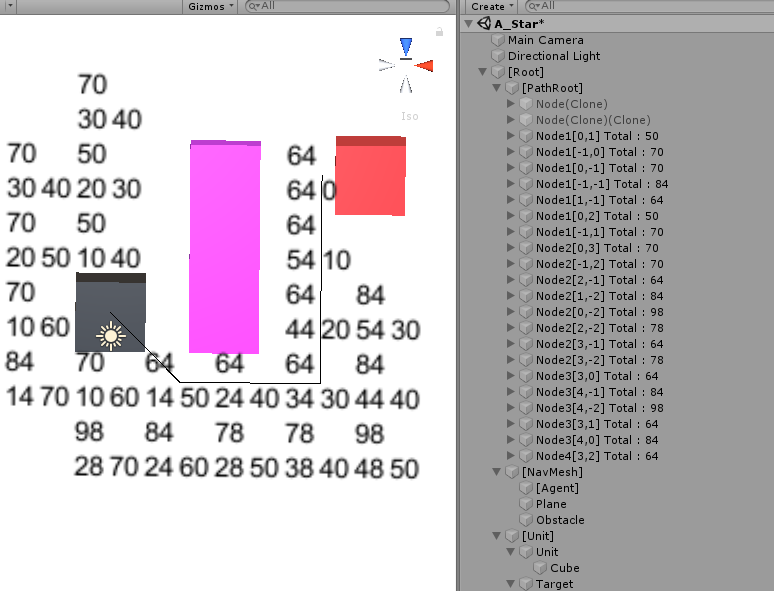
개인적으로는 해당 알고리즘은 길찾는 경우 말고도, 가장 최선의 선택을하는 경우에서도 유용하게 많이 쓰인다. 재귀에 대해서 잘 이해하고 사용하면 코드도 간단하다.
설명이 조금 난해해서 설명을 참고했다.
원본 URL : https://itmining.tistory.com/66
A*(A star) 알고리즘 정의 및 개념
이 글은 PC 버전 TISTORY에 최적화 되어있습니다. 포스팅 순서 1. 개념 및 구현 2. 수도코드(pseudocode) 3. 구현 및 최적화 서론 길찾기 알고리즘은 말 그대로 시작점과 목표점 사이의 최단 거리 길을 찾아주는..
itmining.tistory.com
★★★★☆
'개발 > 기본) 알고리즘' 카테고리의 다른 글
| 알고리즘) 탐욕 알고리즘(Greedy Algorithm) (0) | 2020.06.22 |
|---|---|
| 알고리즘) 트리(Tree)의 종류 (2) | 2020.06.18 |
| 알고리즘) 영향도 알고리즘(Influence Map Algorithm) (0) | 2020.01.22 |
| 알고리즘) 플러드 필 (Flood Fill) (0) | 2020.01.14 |
| 알고리즘) Flocking Algorithm (군중이동 알고리즘) (0) | 2019.12.26 |



댓글